1.3.2. 配列の数値演算¶
1.3.2.1. 要素毎の演算¶
1.3.2.1.1. 基本的な操作¶
スカラーと:
>>> a = np.array([1, 2, 3, 4])
>>> a + 1
array([2, 3, 4, 5])
>>> 2**a
array([ 2, 4, 8, 16])
要素毎の算術演算:
>>> b = np.ones(4) + 1
>>> a - b
array([-1., 0., 1., 2.])
>>> a * b
array([ 2., 4., 6., 8.])
>>> j = np.arange(5)
>>> 2**(j + 1) - j
array([ 2, 3, 6, 13, 28])
これらの操作は、純粋な python でやるより速く実行されます:
>>> a = np.arange(10000)
>>> %timeit a + 1
10000 loops, best of 3: 24.3 us per loop
>>> l = range(10000)
>>> %timeit [i+1 for i in l]
1000 loops, best of 3: 861 us per loop
警告
配列の積は行列の積ではありません:
>>> c = np.ones((3, 3))
>>> c * c # NOT matrix multiplication!
array([[ 1., 1., 1.],
[ 1., 1., 1.],
[ 1., 1., 1.]])
注釈
行列の積:
>>> c.dot(c)
array([[ 3., 3., 3.],
[ 3., 3., 3.],
[ 3., 3., 3.]])
練習問題: 要素毎の演算
単純な要素毎の操作を試してみましょう: 偶数の要素と奇数の要素を要素毎に足してみましょう
%timeitを使って純粋な python での実行結果との実行時間を比較してみましょう。生成してみましょう:
[2**0, 2**1, 2**2, 2**3, 2**4]a_j = 2^(3*j) - j
1.3.2.1.2. その他の操作¶
比較:
>>> a = np.array([1, 2, 3, 4])
>>> b = np.array([4, 2, 2, 4])
>>> a == b
array([False, True, False, True], dtype=bool)
>>> a > b
array([False, False, True, False], dtype=bool)
ちなみに
配列に対する比較:
>>> a = np.array([1, 2, 3, 4])
>>> b = np.array([4, 2, 2, 4])
>>> c = np.array([1, 2, 3, 4])
>>> np.array_equal(a, b)
False
>>> np.array_equal(a, c)
True
論理演算:
>>> a = np.array([1, 1, 0, 0], dtype=bool)
>>> b = np.array([1, 0, 1, 0], dtype=bool)
>>> np.logical_or(a, b)
array([ True, True, True, False], dtype=bool)
>>> np.logical_and(a, b)
array([ True, False, False, False], dtype=bool)
超越関数:
>>> a = np.arange(5)
>>> np.sin(a)
array([ 0. , 0.84147098, 0.90929743, 0.14112001, -0.7568025 ])
>>> np.log(a)
array([ -inf, 0. , 0.69314718, 1.09861229, 1.38629436])
>>> np.exp(a)
array([ 1. , 2.71828183, 7.3890561 , 20.08553692, 54.59815003])
シェイプの不一致
>>> a = np.arange(4)
>>> a + np.array([1, 2])
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: operands could not be broadcast together with shapes (4) (2)
broadcast? これについては 後で 扱います。
転置:
>>> a = np.triu(np.ones((3, 3)), 1) # see help(np.triu)
>>> a
array([[ 0., 1., 1.],
[ 0., 0., 1.],
[ 0., 0., 0.]])
>>> a.T
array([[ 0., 0., 0.],
[ 1., 0., 0.],
[ 1., 1., 0.]])
警告
転置はビューです
結果として、以下のコードは 間違っています そして 行列は対称になりません:
>>> a += a.T
小さい配列に対しては動作するかもしれません(バッファリングによって)、しかし、大きな配列に対しては失敗します、どうなるか予測することは難しいでしょう。
注釈
線形代数
numpy.linalg サブモジュールは例えば線形系の求解、特異値分解等の基本的な線形代数演算を実装しています。しかし、効率的なルーチンを利用してコンパイルされているかについては保証されていません、そのため scipy.linalg を利用することを推奨します、詳細については 線形代数演算: scipy.linalg の節を参照して下さい。
その他の操作についての練習問題
np.allcloseのヘルプを見てみましょう。どういうときに便利でしょうか。
np.triuやnp.trilのヘルプをみてみましょう。
1.3.2.2. 基本的な縮約操作¶
1.3.2.2.1. 総和を計算¶
>>> x = np.array([1, 2, 3, 4])
>>> np.sum(x)
10
>>> x.sum()
10
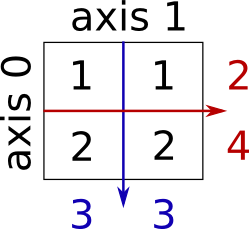
行や列毎の和:
>>> x = np.array([[1, 1], [2, 2]])
>>> x
array([[1, 1],
[2, 2]])
>>> x.sum(axis=0) # columns (first dimension)
array([3, 3])
>>> x[:, 0].sum(), x[:, 1].sum()
(3, 3)
>>> x.sum(axis=1) # rows (second dimension)
array([2, 4])
>>> x[0, :].sum(), x[1, :].sum()
(2, 4)
ちなみに
同じ発想を高次元で:
>>> x = np.random.rand(2, 2, 2)
>>> x.sum(axis=2)[0, 1]
1.14764...
>>> x[0, 1, :].sum()
1.14764...
1.3.2.2.2. その他の縮約操作¶
— 同じように動作するもの (そして axis= 引数をとる)
極値:
>>> x = np.array([1, 3, 2])
>>> x.min()
1
>>> x.max()
3
>>> x.argmin() # index of minimum
0
>>> x.argmax() # index of maximum
1
論理演算:
>>> np.all([True, True, False])
False
>>> np.any([True, True, False])
True
注釈
配列比較にも利用できる:
>>> a = np.zeros((100, 100))
>>> np.any(a != 0)
False
>>> np.all(a == a)
True
>>> a = np.array([1, 2, 3, 2])
>>> b = np.array([2, 2, 3, 2])
>>> c = np.array([6, 4, 4, 5])
>>> ((a <= b) & (b <= c)).all()
True
統計:
>>> x = np.array([1, 2, 3, 1])
>>> y = np.array([[1, 2, 3], [5, 6, 1]])
>>> x.mean()
1.75
>>> np.median(x)
1.5
>>> np.median(y, axis=-1) # last axis
array([ 2., 5.])
>>> x.std() # full population standard dev.
0.82915619758884995
... など他にも (やっていく内に学んでいきましょう)。
練習問題: 縮約操作
ここまで出てきた中に
sumがありました、他にはどうんあ関数があると思いますか?
sumとcumsumの違いは何でしょうか?
演習例: データ統計
populations.txt のデータには北カナダでの20年分の野うさぎ hare と大山猫 lynx (そして 人参 carrot) の個体数が書かれています。
データをエディタでみることもできますし、IPython (shell でも notebook でも構いません) でみることもできます:
In [1]: !cat data/populations.txt
まず、Numpy の配列としてデータを読み込みます:
>>> data = np.loadtxt('data/populations.txt')
>>> year, hares, lynxes, carrots = data.T # trick: columns to variables
次にプロットしましょう:
>>> from matplotlib import pyplot as plt
>>> plt.axes([0.2, 0.1, 0.5, 0.8])
>>> plt.plot(year, hares, year, lynxes, year, carrots)
>>> plt.legend(('Hare', 'Lynx', 'Carrot'), loc=(1.05, 0.5))
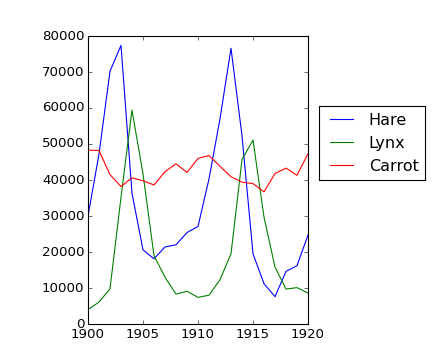
個体数を時間に対して平均:
>>> populations = data[:, 1:]
>>> populations.mean(axis=0)
array([ 34080.95238095, 20166.66666667, 42400. ])
標本標準偏差:
>>> populations.std(axis=0)
array([ 20897.90645809, 16254.59153691, 3322.50622558])
各年でどの種が最大の個体数でしたか?:
>>> np.argmax(populations, axis=1)
array([2, 2, 0, 0, 1, 1, 2, 2, 2, 2, 2, 2, 0, 0, 0, 1, 2, 2, 2, 2, 2])
演習例: ランダムウォークアルゴリズムによる拡散

ちなみに
1次元のランダムウォーク過程を考えます: 各時間ステップでウォーカーは右か左に等確率でジャンプします。
t 後にウォーカーが原点から右か左に典型的にどれだけ離れるのか興味があります。たくさんの酔っ払いをシミュレーションして法則を見つけましょう、そしてここで配列をうまく使ってみます: “stories” という2次元配列を作ります(それぞれのウォーカーはストーリーを持っています) 次元の一つは方向で、残りが時間です。

>>> n_stories = 1000 # number of walkers
>>> t_max = 200 # time during which we follow the walker
全ての試行で 1 か -1 のどちらかをランダムに選択します:
>>> t = np.arange(t_max)
>>> steps = 2 * np.random.random_integers(0, 1, (n_stories, t_max)) - 1
>>> np.unique(steps) # Verification: all steps are 1 or -1
array([-1, 1])
各試行を時間に沿って和をとることで足取りを辿ります:
>>> positions = np.cumsum(steps, axis=1) # axis = 1: dimension of time
>>> sq_distance = positions**2
ストーリーの軸に沿って平均を求めます:
>>> mean_sq_distance = np.mean(sq_distance, axis=0)
結果をプロットします:
>>> plt.figure(figsize=(4, 3))
<matplotlib.figure.Figure object at ...>
>>> plt.plot(t, np.sqrt(mean_sq_distance), 'g.', t, np.sqrt(t), 'y-')
[<matplotlib.lines.Line2D object at ...>, <matplotlib.lines.Line2D object at ...>]
>>> plt.xlabel(r"$t$")
<matplotlib.text.Text object at ...>
>>> plt.ylabel(r"$\sqrt{\langle (\delta x)^2 \rangle}$")
<matplotlib.text.Text object at ...>
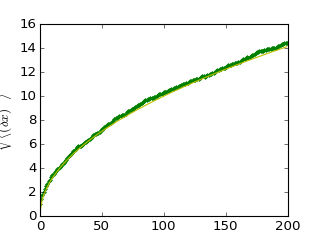
平均二乗距離は時間の平方根で成長する、という物理でよくしられた結果に遭遇します。
1.3.2.3. ブロードキャスト¶
numpyの配列の基本演算 (加算等) は要素毎これは同じサイズの配列で動作します。
にも関わらず 異なるサイズの配列に対しても操作することができますNumpy がこれらの配列全てを変換して同じサイズを持つようにできる場合においては: この変換は broadcasting と呼ばれます。
この下の画像はブロードキャストの例を示しています:
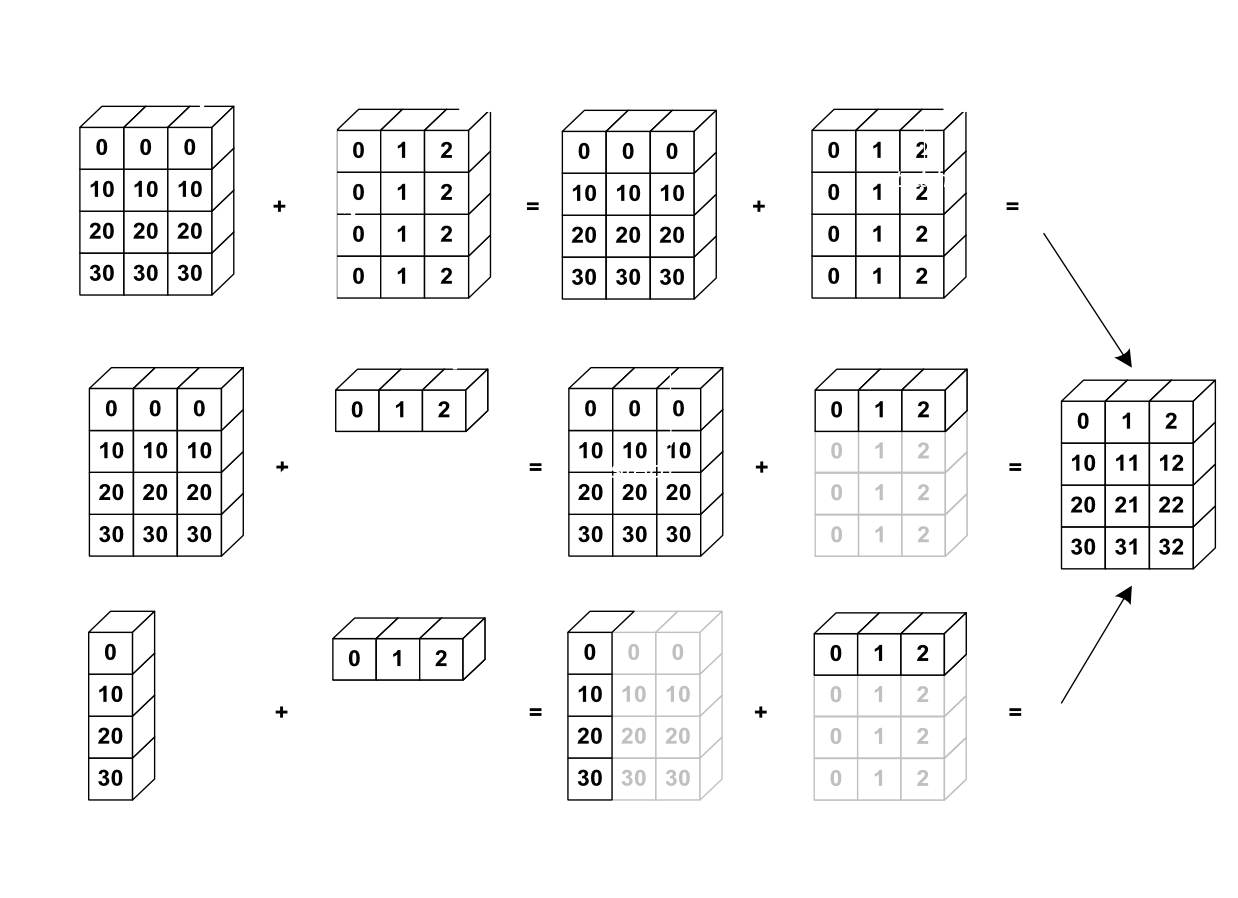
確認してみましょう:
>>> a = np.tile(np.arange(0, 40, 10), (3, 1)).T
>>> a
array([[ 0, 0, 0],
[10, 10, 10],
[20, 20, 20],
[30, 30, 30]])
>>> b = np.array([0, 1, 2])
>>> a + b
array([[ 0, 1, 2],
[10, 11, 12],
[20, 21, 22],
[30, 31, 32]])
実は以前にもブロードキャストを使っていました!:
>>> a = np.ones((4, 5))
>>> a[0] = 2 # we assign an array of dimension 0 to an array of dimension 1
>>> a
array([[ 2., 2., 2., 2., 2.],
[ 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1.]])
便利な技:
>>> a = np.arange(0, 40, 10)
>>> a.shape
(4,)
>>> a = a[:, np.newaxis] # adds a new axis -> 2D array
>>> a.shape
(4, 1)
>>> a
array([[ 0],
[10],
[20],
[30]])
>>> a + b
array([[ 0, 1, 2],
[10, 11, 12],
[20, 21, 22],
[30, 31, 32]])
ちなみに
ブロードキャストは少々不思議に思えるでしょう、しかし入力データより出力データが多い問題を解くような場合自然に使うことができます。
演習例: ブロードキャスティング
ルート 66 での各街 (Chicago, Springfield, Saint-Louis, Tulsa, Oklahoma City, Amarillo, Santa Fe, Albucquerque, Flagstaff そして Los Angeles) 間の距離(マイル)を表わす配列を作ってみましょう.
>>> mileposts = np.array([0, 198, 303, 736, 871, 1175, 1475, 1544,
... 1913, 2448])
>>> distance_array = np.abs(mileposts - mileposts[:, np.newaxis])
>>> distance_array
array([[ 0, 198, 303, 736, 871, 1175, 1475, 1544, 1913, 2448],
[ 198, 0, 105, 538, 673, 977, 1277, 1346, 1715, 2250],
[ 303, 105, 0, 433, 568, 872, 1172, 1241, 1610, 2145],
[ 736, 538, 433, 0, 135, 439, 739, 808, 1177, 1712],
[ 871, 673, 568, 135, 0, 304, 604, 673, 1042, 1577],
[1175, 977, 872, 439, 304, 0, 300, 369, 738, 1273],
[1475, 1277, 1172, 739, 604, 300, 0, 69, 438, 973],
[1544, 1346, 1241, 808, 673, 369, 69, 0, 369, 904],
[1913, 1715, 1610, 1177, 1042, 738, 438, 369, 0, 535],
[2448, 2250, 2145, 1712, 1577, 1273, 973, 904, 535, 0]])
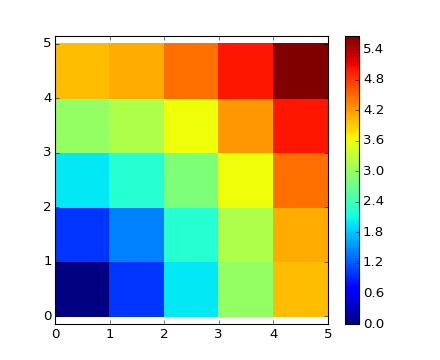
たくさんの格子やネットワークで構成されているような問題でもブロードキャストを使うことができます。例えば、10x10 の格子上の点の原点からの距離を計算したい場合、こうして計算できます
>>> x, y = np.arange(5), np.arange(5)[:, np.newaxis]
>>> distance = np.sqrt(x ** 2 + y ** 2)
>>> distance
array([[ 0. , 1. , 2. , 3. , 4. ],
[ 1. , 1.41421356, 2.23606798, 3.16227766, 4.12310563],
[ 2. , 2.23606798, 2.82842712, 3.60555128, 4.47213595],
[ 3. , 3.16227766, 3.60555128, 4.24264069, 5. ],
[ 4. , 4.12310563, 4.47213595, 5. , 5.65685425]])
色をつけてみると:
>>> plt.pcolor(distance)
>>> plt.colorbar()
所見 : numpy.ogrid 関数は、2つの”代表的次元” を与えることで、前の例の x, y ベクトルを直接作りだすことができます:
>>> x, y = np.ogrid[0:5, 0:5]
>>> x, y
(array([[0],
[1],
[2],
[3],
[4]]), array([[0, 1, 2, 3, 4]]))
>>> x.shape, y.shape
((5, 1), (1, 5))
>>> distance = np.sqrt(x ** 2 + y ** 2)
ちなみに
これからわかるように np.ogrid は格子状の計算を扱うのにとても便利です。一方 np.mgrid は完全なインデクスを持つ行列を直接提供します。これはブロードキャストの恩恵を受けられない(もしくは受けたくない)場合に使うことができます:
>>> x, y = np.mgrid[0:4, 0:4]
>>> x
array([[0, 0, 0, 0],
[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3]])
>>> y
array([[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3]])
1.3.2.4. 配列のシェイプ操作¶
1.3.2.4.1. 平坦化¶
>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> a.ravel()
array([1, 2, 3, 4, 5, 6])
>>> a.T
array([[1, 4],
[2, 5],
[3, 6]])
>>> a.T.ravel()
array([1, 4, 2, 5, 3, 6])
高次元: 最後の次元が”最初に”ほどかれます。
1.3.2.4.2. シェイプの変更¶
平坦化の逆操作:
>>> a.shape
(2, 3)
>>> b = a.ravel()
>>> b = b.reshape((2, 3))
>>> b
array([[1, 2, 3],
[4, 5, 6]])
あるいは、
>>> a.reshape((2, -1)) # unspecified (-1) value is inferred
array([[1, 2, 3],
[4, 5, 6]])
警告
ndarray.reshape はビューかコピーを返す 可能性があります (help(np.reshape) と比べてみて下さい))
ちなみに
>>> b[0, 0] = 99
>>> a
array([[99, 2, 3],
[ 4, 5, 6]])
注意: reshape は コピーを返すかもしれません!:
>>> a = np.zeros((3, 2))
>>> b = a.T.reshape(3*2)
>>> b[0] = 9
>>> a
array([[ 0., 0.],
[ 0., 0.],
[ 0., 0.]])
理解するためには numpy 配列のメモリレイアウトについて学ぶ必要があります。
1.3.2.4.3. 次元の追加¶
np.newaxis オブジェクトをインデクシングに使うと、配列に軸を追加することができます(このことは上にあるブロードキャスティングの節で触れています):
>>> z = np.array([1, 2, 3])
>>> z
array([1, 2, 3])
>>> z[:, np.newaxis]
array([[1],
[2],
[3]])
>>> z[np.newaxis, :]
array([[1, 2, 3]])
1.3.2.4.4. 次元の入れ替え¶
>>> a = np.arange(4*3*2).reshape(4, 3, 2)
>>> a.shape
(4, 3, 2)
>>> a[0, 2, 1]
5
>>> b = a.transpose(1, 2, 0)
>>> b.shape
(3, 2, 4)
>>> b[2, 1, 0]
5
もちろんビューを作ります:
>>> b[2, 1, 0] = -1
>>> a[0, 2, 1]
-1
1.3.2.4.5. リサイズ¶
配列のサイズは ndarray.resize によって変えることもできます:
>>> a = np.arange(4)
>>> a.resize((8,))
>>> a
array([0, 1, 2, 3, 0, 0, 0, 0])
しかし、参照先はどこかにある必要があります。
>>> b = a
>>> a.resize((4,))
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: cannot resize an array that has been referenced or is
referencing another array in this way. Use the resize function
練習問題: シェイプ操作
reshapeの docstring をみてみましょう、特に notes 節にはコピーとビューについてに詳しい情報があります。ravelの替わりにflattenを使ってみましょう。違いはなんでしょうか。(ヒント: どちらがビューを返して、どちらがコピーを返すのか確認してみましょう)transposeで次元の入れ替えを試してみましょう。
1.3.2.5. データのソート¶
軸に沿ってソート:
>>> a = np.array([[4, 3, 5], [1, 2, 1]])
>>> b = np.sort(a, axis=1)
>>> b
array([[3, 4, 5],
[1, 1, 2]])
注釈
各行を別々にソート!
インプレースにソート:
>>> a.sort(axis=1)
>>> a
array([[3, 4, 5],
[1, 1, 2]])
ファンシーインデクスを使ってソート:
>>> a = np.array([4, 3, 1, 2])
>>> j = np.argsort(a)
>>> j
array([2, 3, 1, 0])
>>> a[j]
array([1, 2, 3, 4])
最小値と最大値を見つける:
>>> a = np.array([4, 3, 1, 2])
>>> j_max = np.argmax(a)
>>> j_min = np.argmin(a)
>>> j_max, j_min
(0, 2)
練習問題: ソート
インプレースなソートとアウトオブプレースなソートの両方を試してみましょう。
dtype が異なる配列を作ってそれらをソートしてみましょう。
allかarray_equalを使って結果を確認してみましょう。
np.random.shuffleで手早くソートできる入力を作ってみましょう。
rabelとsortそしてreshapeを組み合わせてみましょう。
axisキーワードをsortに対して使い、前の演習問題を書き直してみましょう。
1.3.2.6. まとめ¶
何を知っていれば一通り覚えたことになる?
配列の作り方を知っている:
array,arange,ones,zeros。配列のシェイプを
array.shapeを使って知る、次にスライスで配列の異なるビューを得る:array[::2]等。配列のシェイプをreshapeを使って調整したり、ravelを使って平坦化する。マスクを使って配列の一部を得たり、変更する:
>>> a[a < 0] = 0
平均や最大値を求める (
array.max(),array.mean()) といった様々な配列の操作について知っている。 全てを知っている必要はありませんが、反射的にドキュメントを検索できる (online docs,help(),lookfor())!!より高度な利用法を身につけるには: 整数配列によるインデックスを習得する、ブロードキャストも同様。様々な配列操作を扱う Numpy の関数についてよく知る
急いで読みたい人は
エコシステムを知るために、講義を素早く進めたい場合、次の Matplotlib: 作図 まで読み飛ばしてもかまいません。
この入門章の残りの部分は必ず必要というわけではありません。しかし、後に戻ってきて完了することになるでしょう 演習問題 も同様です。
